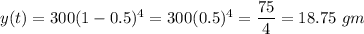Question

Cobalt-60 has a half-life of about 5 years. How many grams of 300 g sample well remain after 20 years?

Answer 1

20/5 = 4 half lives

so

300 * (1/2)^4
= 300 * 0.0625
=18.75 grams

Answer 2

After 20 years 18.75 gm of sample will remain.

Explanation:

This is the case of an exponential decay of Cobalt-60. The function for exponential decay is,

`y(t)=a(1-r)^t`

where,

y(t) = amount left after time t

a = initial amount = 300 g

r = rate of decay = 0.5 (as the sample is getting halved each time)

t = number of periods =
`(20)/(5)=4` (as we have to convert the period in terms of half lives)

Putting the values,

`y(t)=300(1-0.5)^4=300(0.5)^(4)=(75)/(4)=18.75\ gm`