Question

Using technology, determine the monthly payment on a 6 year loan of $15,250 at 3.5% compounded monthly. Round your answer to the nearest cent.

a. $234.75c. $582.70

b. $235.13d. $590.05

Answer 1

235.13 hope it helps

Answer 2

Option 3 or b - The monthly payment is $235.13.

Explanation:

Given : A 6 year loan of $15,250 at 3.5% compounded monthly.

To find : Monthly payment ?

Solution :

The formula to find monthly payment is

`M=\frac{\text{Amount}}{\text{Discount factor}}`

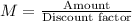
Discount factor is
`D=(1-(1+i)^(-n))/(i)`

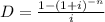
Substitute in the formula,

`M=(A)/((1-(1+i)^(-n))/(i))`

`M=(A* i)/(1-(1+i)^(-n))`

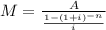
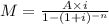
where, A is the amount A=$15250

r is the rate = 3.5%=0.035 compounded monthly

`i=(r)/(12)=\farc{0.035}{12}=0.00291`

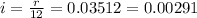
time t=6 years

Time in months
`n=t* 12=6* 12=72`

Substitute all the values in the formula,

`M=(15250* 0.00291)/(1-(1+0.00291)^(-72))`

`M=(44.479)/(1-(1.00291)^(-72))`

`M=(44.479)/(1-0.8112)`

`M=(44.479)/(0.18916)`

`M=235.13`

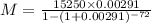
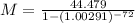
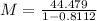
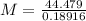
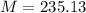
Therefore, The monthly payment is $235.13.

So, Option 3 or b is correct.