Question

Need help answering these questions to pass

Answer 1

Ratio of Area of Rectangle ABEF to Rectangle ACDF is 2 : 3

Area of rectangle ABEF is 10√41 units²

Perimeter of rectangle BCDE is ( 10 + 2√41 ) units²

Explanation:

Given: ABEF and BCDE and ACDF are rectangles.

coordinates of F( 5 , 2 ) , E( 11 , 10 ) , D( 14 , 14 ) and A( 0 , 6 )

To find: Ratio of Area of Rectangle ABEF to Rectangle ACDF

Area of rectangle ABEF

Perimeter of BCDE.

We know that, Area of Rectangle = Length × Width

In rectangle ABEF

length = FE =
`√((11-5)^2+(10-2)^2)=√(6^2+8^2)=√(36+64)=10\,units`

Width = FA

Area of Rectangle ABEF = FE × FA = ( 10 × FA ) units²

In rectangle ACDF

length = FD =
`√((14-5)^2+(14-2)^2)=√(9^2+12^2)=√(81+144)=15\,units`

Width = FA

Area of Rectangle ACDF = FD × FA = ( 15 × FA ) units²

`(Area\:of\:Rectangle\:ABEF )/(Area\:of\:Rectangle\:ACDF)=(10* FA)/(15* FA)=(2)/(3)`

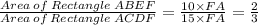
Thus, Ratio of Area of Rectangle ABEF to Rectangle ACDF is 2 : 3

In rectangle ABEF

length = FE = 10 units (from above)

Width = FA =
`√((0-5)^2+(6-2)^2)=√((-5)^2+4^2)=√(25+16)=√(41)\,units`

Area of Rectangle ABEF = FE × FA = 10 × √41 = 10√41 units²

Thus, Area of rectangle ABEF is 10√41 units²

In rectangle BCDE

length = DE =
`√((14-11)^2+(14-10)^2)=√(3^2+4^2)=√(9+16)=√(25)=5\,units`

Width = CD = FA = √41 units

Perimeter of Rectangle BCDE = 2 × ( DE + CD ) = 2 × (5 + √41) = ( 10 + 2√41 ) units²

Thus, Perimeter of rectangle BCDE is ( 10 + 2√41 ) units²