Answer:
a)
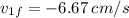
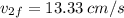
b)
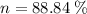
Step-by-step explanation:
a) Applying the conservation of momentum, we have:
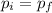
p(i) is the initial momentum. In our case is due to the 5 g object.
p(f) is the final momentum. Here, both objects contribute.
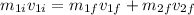
Where:
- m(1) is 5 g
- m(1) is 10 g
- v(1i) is the initial velocity 20 cm/s or 0.2 m/s
To find both final velocities we will need another equation, let's use the conservation of kinetic energy.
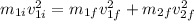
So we have a system of equations:
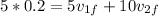 (1)
(1)
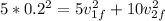 (2)
(2)
Solving this system we get:
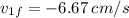
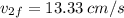
b) The fraction of the initial kinetic energy transferred is:
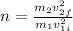
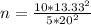
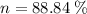
I hope it helps you!