Question

A consolidated-drained triaxial test is carried out on a sand specimen that is subjected to 80 kN/m2 confining pressure. The vertical deviator stress was increased slowly such that there is no built-up of pore water pressure within the specimen. The specimen failed when the addition axial stress reached 240 kN/m2. Find the friction angle of the sand. If another identical sand specimen was subjected to 150 kN/m2 confining pressure, what would be the deviator stress at failure.

Answer 1

a) the friction angle of the sand is 36.87°

b) the deviator stress at failure is 450 kN/m³

Step-by-step explanation:

Given the data in the question;

For a consolidated drained test

The effective major principle stresses

σ₃ = σ₃' = 80 kN/m²

and

σ₁' = σ₃' + (Δσ
`_(d)`)
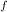`_(f)` = 80 kN/m² + 240 kN/m² = 320 kN/m²

now

a) friction angle of the sand

σ₁' = σ₃'tan²( 45° + Ф/2' ) + 2c' tan( 45° + Ф/2 )

for sand; c' = 0

so

σ₁' = σ₃'tan²( 45° + Ф/2' )

we substitute

320 = 80 tan²( 45° + Ф/2' )

Ф' = 2 × [ tan⁻¹ (√
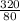`(320)/(80)`) - 45° ]

Ф' = 2 × [ 63.4349° - 45° ]

Ф' = 2 × 18.4349

Ф' = 36.87°

Therefore, the friction angle of the sand is 36.87°

b) deviator stress

σ₁' = σ₃'tan²( 45° + Ф/2' )

σ₁' = σ₃' + (Δσ
`_(d)`)
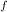`_(f)` = σ₃'tan²( 45° + Ф/2' )

σ₃' + (Δσ
`_(d)`)
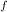`_(f)` = σ₃'tan²( 45° + Ф/2' ) 3.597

150 + (Δσ
`_(d)`)
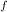`_(f)` = 150tan²( 45° + 36.87°/2 )

150 + (Δσ
`_(d)`)
`_(f)` = 600

(Δσ
`_(d)`)
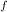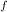`_(f)` = 600 - 150

(Δσ
`_(d)`)
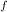`_(f)` = 450 kN/m³

Therefore, the deviator stress at failure is 450 kN/m³