Let:
A1 = Area of triangle A
A2 = Area of triangle B
Since the dimensions of triangle B are twice the dimensions of triangle A, then:
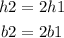
Where:
h1 = height of triangle A
h2 = height of triangle B
b1 = base of triangle A
b2 = base of triangle B
The area of the triangle B is given by:
![\begin{gathered} A2=(b2\cdot h2)/(2) \\ A2=((2b1\cdot2h1))/(2) \\ A2=2b1\cdot h1 \\ where \\ b1\cdot h1=2A1 \\ b1\cdot h1=2(15\operatorname{cm})=30cm^2 \\ A2=2(30cm^2) \\ A2=60cm^2 \end{gathered}]()
Answer:
60 cm²