Question

The population of country Y is 170 million. The population reaches 340 million 85 years later. At what percent growth is the country increasing (round to the nearest hundredth percent)

Answer 1

We know the country's population is 170 million. After 85 years, it reaches 340 million.

We can use the population growth formula in order to determine the growth rate:

`N=n_o\cdot e^(rt),`

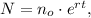
where N is the population after time t, n₀ is the initial population and r is the growth rate (in the same units as t).

In this case, we have an equation for r:

`340=170\cdot e^(r\cdot85),`

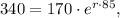
where we have ommited the fact that the numbers given were in the millions since all those zeroes woud have cancelled out at some point when solving the equation.

Let's solve the equation:

`(340)/(170)=e^(r\cdot85),`
`2=e^(r\cdot85),`
`\ln (2)=\ln (e^(r\cdot85)),`
`\ln (2)=r\cdot85,`
`r=(\ln (2))/(85),`
`r\approx0.008154,`

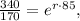
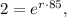
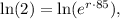
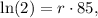
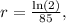
which translates to approximately 0.82%.

In other words, the population grew at a rate of 0.82% per year.