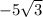Answer:
The roots of the given quadratic function
 is
is
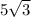 and
and
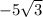
Explanation:
Given: Quadratic function

We have to find the roots of the given quadratic function

Since, roots of the quadratic equation is the points where the value of function is zero.
That is f(x) = 0
Consider the given function

Put f(b) = 0

Simplify , we have,
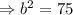
Taking square root both side, we have,
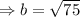
Simplify we have,
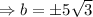
Thus, The roots of the given quadratic function
 is
is
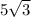 and
and