Answer:
Probability: 0.9405
E(x) = 10.0705
σ = 0.9225
Step-by-step explanation:
Using the binomial distribution, we get that the probability is calculated as
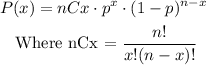
Where n is the number of trials, p is the probability of success, and x is the number of successful trials. In this case, p = 91.55% = 0.9155 and n = 11. Then, the probability is calculated as
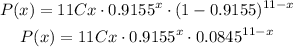
Now, we need to calculate the probability that the player will make 9 or more free throws. This probability is equal to
![\begin{gathered} P(x\ge9)=P(9)+P(10)+P(11) \\ \text{ Where} \\ P(9)=11C9\cdot0.9155^9\cdot0.0845^(11-9)=0.1774 \\ P(10)=11C10\cdot0.9155^^(10)\cdot0.0845^(11-10)=0.3844 \\ P(11)=11C11\cdot0.9155^(11)\cdot0.0845^(11-11)=0.3787 \\ So \\ P(x\ge9)=0.1774+0.3844+0.3787 \\ P(x\ge9)=0.9405 \end{gathered}]()
Therefore, the probability is equal to 0.9405
On the other hand, the expected value and the standard deviation are equal to
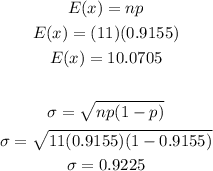
Therefore, the answers are
Probability: 0.9405
E(x) = 10.0705
σ = 0.9225