1 Answer

Ask a Question

Zbigniew Wazeliniak · Answer 1 · 2023-12-23T10:25:15+0000

Solution:

Given the data below:

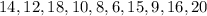
1) The range is the spread of data from the lowest to the highest value in the distribution.

In other words,

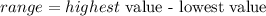
$range=highest\text{ value - lowest value}$

In this case,

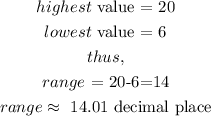
$\begin{gathered} highest\text{ value = 20} \\ lowest\text{ value = 6} \\ thus, \\ range\text{ = 20-6=14} \\ range\approx\text{ 14.0\lparen 1 decimal place\rparen} \end{gathered}$

Thus, the range is 14.0 (1 decimal place)

2) Population variance:

The population variance is expressed as

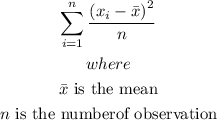
$\begin{gathered} \sum_(i=1)^n\frac{\left(x_i-\bar{x}\right)^2}{n} \\ where \\ \bar{x}\text{ is the mean} \\ n\text{ is the numberof observation} \end{gathered}$

Thus, we have

$\begin{gathered} ((14-12.8)^2+(12-12.8)^2+(18-12.8)^2+(10-12.8)^2+(8-12.8)^2+(6-12.8)^2+(15-12.8)^2+(9-12.8)^2+(16-12.8)^2+(20-12.8)^2)/(10) \\ =(187.6)/(10) \\ =18.76 \\ population\text{ variance}\approx18.8\text{ \lparen1 decimal place\rparen} \end{gathered}$

Thus, the population variance is 18.8 (1 decimal place)

3) Standard deviation:

the standrard deviation is the square root of the variance.

Hence, we have

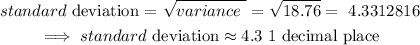
$\begin{gathered} standard\text{ deviation = }\sqrt{variance\text{ }}=√(18.76)=\text{ }4.3312816 \\ \implies standard\text{ deviation}\approx4.3\text{ \lparen1 decimal place\rparen} \end{gathered}$

Hence, the standard deviation is 4.3 (1 decimal place)

0 Comments

Your comment on this question:

Your answer

1 Answer

0 Comments

Your comment on this answer:

Other Questions