Question

Three students made claims about y.Each student has provided his or her work to support their claim, as shown below.analyze the student's work and identify which part of his or her claim is correct or incorrect? Select TWO that apply.

Answer 1

C and E

1) Let's evaluate that so we can find out the answers:

`\begin{gathered} y^{(3)/(2)}=(y^{(1)/(3)}\cdot y^{(1)/(3)}) \\ y^{(3)/(2)}\\e y^{(1+1)/(3)}\Rightarrow y^{(3)/(2)}\\e y^{(2)/(3)} \end{gathered}`

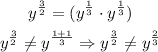
So Student 1 has come to a false conclusion.

• Student 2

`\begin{gathered} y^{(3)/(2)}=(y\cdot y\cdot y)^{(1)/(2)}\Rightarrow y^{(3)/(2)}=(y^3)^{(1)/(2)}\Rightarrow y^{(3)/(2)}=y^{(3)/(2)} \\ (\sqrt[]{y\cdot y\cdot y})=(y^{(3)/(2)})=(\sqrt[]{y^3}) \end{gathered}`

Note that we can add the exponents of a product of power with the same exponent. Also, rational exponents indicate a radical.

So Student 2 has come to a True conclusion

• Student 3

`\begin{gathered} y^{(3)/(2)}=(y^{(1)/(2)+(1)/(2)+(1)/(2)})\Rightarrow y^{(3)/(2)}=y^{(3)/(2)} \\ (\sqrt[]{y}\cdot\sqrt[]{y}\cdot\sqrt[]{y})=(\sqrt[]{y}^3)\text{ =}y^{(3*1)/(2)}=y^{(3)/(2)} \end{gathered}`

Since by the exponents' property the sum of the exponents within a product of same base powers and rational exponents rewritten as radicals, we can state that Studen t 3 has come up to a true conclusion.

3) Hence, the answers are:

C and E