Question

A charging bull elephant with a mass of 5230 kg comes directly toward you with a speed of 4.45 m/s. You toss a 0.150-kg rubber ball at the elephant with a speed of 7.91 m/s. (a) When the ball bounces back toward you, what is its speed? (b) How do you account for the fact that the ball’s kinetic energy has increased

Answer 1

You have to add the speed of that ball plus the speed is running so 4.45 + 7.91= 12.36m/s

Answer 2

Let us consider the masses of elephant and rubber ball was denoted as-

`m_(1) \ and\ m_(2) \ respectively`

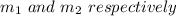
Let the initial velocity of the elephant and rubber ball is denoted as -

`u_(1) \ and\ u_(2)\ respectively`

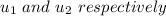
Let the final velocities of the elephant and rubber ball is denoted as-

`v_(1) \ and\ v_(2) \ respectively`

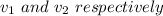
As per the question-

`m_(1) = 5230 kg`
`u_(1) =4.45 m/s`

`m_(2) =0.150 kg`
`u_(2) =7.91 m/s`

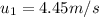
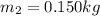
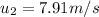
We are asked to calculate the velocities of rubber ball and charged elephant.

From law of conservation of momentum and kinetic energy, we know that-

First we have to calculate the velocity of elephant.

`v_(1) =\frac{m_(1)- m_(2)} {m_(1)+ m_(2)}*u_(1) +\frac{2m_(2)} {m_(1)+ m_(2)}*u_(2)`

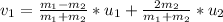
`v_(1) =(5230-0.150)/(5230+0.150)*[4.45] +(2*0.150)/(5230+0.150) *[-7.91]\\` [ Here the velocity of rubber ball is taken as negative as it is opposite to the direction of motion of elephant.]

`v_(1) =(5229.85)/(5230.15) *[4.45]-(0.3)/(5230.15) *[7.91]`

`v_(1) =4.449291034m/s`

Now we have to calculate velocity of rubber ball.

`v_(2) =\frac{m_(2)- m_(1)} {m_(1)+ m_(2)}*u_(2) +\frac{2m_(1)} {m_(1)+ m_(2)} * u_(1)`

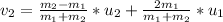
`v_(2) =(0.150-5230)/(5230+0.150) *[-7.91]+(2*5230)/(5230+.150) *[4.45]`

`v_(2) =(-5229.85)/(5230.15) *[-7.91]+(10460)/(5230.15) *[4.45]`

`v_(2) =16.80929103 m/s`

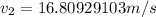
Here we see that velocity of rubber ball is increased.

The kinetic energy of the rubber ball is given as -

`kinetic energy [K.E]=(1)/(2) mv^2`

As the velocity of the ball is increased,hence, its kinetic energy is increased.