Question

write the equation of a line perpindicular to 2x-7y=-6 that passes through the point (-2,6). simplify your answer.

Answer 1

If the two lines are perpendicular then the products of thier slope is ( -1 )

The general form of equation of line :

`y-y_1=m(x-x_1)`

where, m = slope, (x1, y1) are the passing point

The given equation of line : 2x - 7y = -6

Simplify in the general form

`\begin{gathered} 2x-7y=-6 \\ 2x+6=7y \\ 7y=2x+6 \\ y=(2)/(7)x+(6)/(7) \end{gathered}`

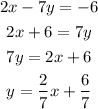
On comparing with the general form of line, we get slope = 2/7

Let the slope of the perpendicular line is m

Thus, from the slope creteria of perpendicular line : m(2/7)=-1

`\begin{gathered} m((2)/(7))=-1 \\ m=(-7)/(2) \end{gathered}`

Substitute the passing point(-2,6) and slope m = -7/2 in the equation of line.

`\begin{gathered} y-y_1=m(x-x_1) \\ y-6=(-7)/(2)(x-(-2)) \\ y-6=(-7)/(2)(x\text{ +2)} \\ y-6=(-7)/(2)x-(-14)/(2) \\ y=-(7)/(2)x+7+6 \\ y=(-7)/(2)x+13 \\ 2y=-7x+26 \\ 7x+2y=26 \end{gathered}`

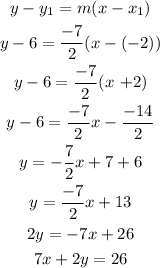
Equation of perpendicular line is 7x + 2y = 26

Answer : 7x + 2y = 26