Question

6) A sample of water is being cooled according to the formula is given by

C(t)= 80 – 2t, where t represents the number of minutes the water is cooled,

and C measures the corresponding temperature in degrees Centigrade. The

cooling period ends when the water freezes (0°). Determine the relevant

domain and range for this function.

Determine the relevant Domain and relevant Range for this function. Use

interval notation.

Answer 1

The relevant domain for the given function is [0, ∞) and the relevant range is [0, 80].

Step-by-step explanation:

The given formula represents the temperature of a sample of water as it is being cooled over time. The formula C(t) = 80 - 2t represents the temperature in degrees Centigrade, where t is the number of minutes the water is cooled.

To determine the relevant domain and range for this function:

1. The domain represents all possible values of t, which in this case is the number of minutes the water is cooled. Since temperature cannot be measured for negative values of t (as it represents the future), the domain of this function is t ≥ 0.
2. The range represents all possible temperature values. Since the temperature C(t) is given by 80 - 2t, the highest temperature is 80°C when t = 0, and the lowest temperature is 0°C when t = 40.

Therefore, the relevant domain for this function is [0, ∞) and the relevant range is [0, 80].

Answer 2

Relevant domain: [0 40]

Relevant range: [0 80]

Step-by-step explanation:

We have the following function:

`C(t) = 80 - 2t`

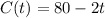
In which C(t) is the water temperature.

t is the time.

The colling period ends when the water freezes (0°).

So it freezes after t minutes, and t is found when C(t) = 0. So

`C(t) = 80 - 2t`

`80 - 2t = 0`

`2t = 80`

`t = (80)/(2)`

`t = 40`

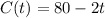
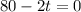
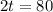
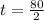
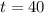
Relevant domain:

Input value of the function, which is in minutes. So between 0(initial) and 40(when the water freezes).

Relevant range:

Initial temperature, which is C(0) = 80, until it freezes, 0. So from 0 to 80.