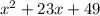Question

A rectangle is shown with length x + 10 and width 2 x +5. The inside of the rectangle is shaded other than an unshaded square with length x + 1 and width x + 1. Write an expression for the area of the shaded region in its simplest form. Show all of your steps.

Answer 1

Given:

The dimension rectangle is length l = x + 10 and width w = 2x + 5.

The side of the square is a = x + 1.

Step-by-step explanation:

The formula for the area of rectangle is,

`A=l\cdot w`

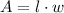
Determine the area of the rectangle.

`\begin{gathered} A=(x+10)(2x+5) \\ =2x^2+5x+20x+50 \\ =2x^2+25x+50 \end{gathered}`

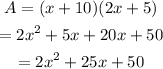
Determine the area of square.

`\begin{gathered} A^(\prime)=(a)^2 \\ =(x+1)^2 \\ =x^2+2x+1 \end{gathered}`

The area of shaded region is equal to difference of area of rectangle and area of square.

Determine the area of shaded region.

`\begin{gathered} A_{\text{shaded}}=A-A^(\prime) \\ =2x^2+25x+50-(x^2+2x+1) \\ =x^2+23x+49 \end{gathered}`

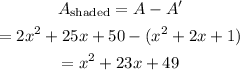
So expression for area of shaded region is,

`x^2+23x+49`