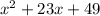Given:
The dimension rectangle is length l = x + 10 and width w = 2x + 5.
The side of the square is a = x + 1.
Step-by-step explanation:
The formula for the area of rectangle is,
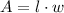
Determine the area of the rectangle.
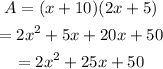
Determine the area of square.
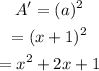
The area of shaded region is equal to difference of area of rectangle and area of square.
Determine the area of shaded region.
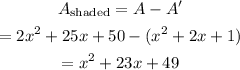
So expression for area of shaded region is,