Question

On the package for a certain brand of spinach seeds there is a guarantee that, if the printed instructions are followed, of planted seeds will germinate. A random sample of seeds is chosen. If these seeds are planted according to the instructions, find the probability that of them germinate.

Answer 1

The question is incomplete. Here is the complete question.

On the package for a certain brand of spinach seeds there is a guarantee that, if the printed instructions are followed, 63% of planted seeds will germinate. A random sample of 9 seeds is chosen. If these seeds are planted according to the instructions, find the probability that 4 or 5 of them germinate. Do not round your intermiediate computations, and round your answer to three decimal places.

Answer: P(4<X<5) = 0.624

Explanation: The probability of a seed germinate is a Binomial Distribution, i.e., a discrete probability distribution of the number of successes in a sequence of n independents experiments.

This distribution can be approximated to normal distribution by determining the values of mean and standard deviation population:

`\mu=np`

`\sigma=√(np(1-p))`

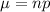
where

n is the sample quantity

p is proportion of successes

For the spinach seeds:

Mean is

`\mu=9(0.65)`

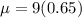
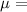`\mu=` 5.85

Standard deviation is

`\sigma=√(9.0.65(1-0.65))`

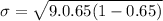
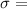`\sigma=` 1.431

Now, use

`z=(x-\mu)/(\sigma)`

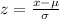
to convert into a standard normal distribution.

The probability we want is between 2 values: P(4<X<5).

Therefore, we have to convert those two values:

For X = 4:

`z=(4-5.85)/(1.431)`

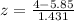
z = -1.29

For X = 5:

`z=(5-5.85)/(1.431)`

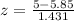
z = -0.59

Using z-table:

P(X>4) = 1 - P(z< -1.29) = 0.9015

P(X<5) = P(z< -0.59) = 0.2776

The probability will be

P(4<X<5) = P(X>4) - P(X<5)

P(4<X<5) = 0.9015 - 0.2776

P(4<X<5) = 0.624

The probability of 4 or 5 seeds germinate is 0.624.