The ordered pairs that satisfy the functions
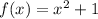 and
and
 are: (0, 1), (1, 2), (-1, 2), (2, 5), (-2, 5) for f(x), (0, -1), (1, 0), (-1, 0), (2, 3), (-2, 3) for g(x), and (0, 0), (1, 2), (-1, 2), (2, 8), (-2, 8) for f(x) + g(x).
are: (0, 1), (1, 2), (-1, 2), (2, 5), (-2, 5) for f(x), (0, -1), (1, 0), (-1, 0), (2, 3), (-2, 3) for g(x), and (0, 0), (1, 2), (-1, 2), (2, 8), (-2, 8) for f(x) + g(x).
The given functions are
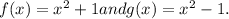
To find ordered pairs that satisfy these functions, we can substitute different values of x and calculate the corresponding y values.
For f(x):
When x = 0, f(0) = 0^2 + 1 = 1, so we have the ordered pair (0, 1).
When x = 1, f(1) = 1^2 + 1 = 2, so we have the ordered pair (1, 2).
When x = -1, f(-1) = (-1)^2 + 1 = 2, so we have the ordered pair (-1, 2).
When x = 2, f(2) = 2^2 + 1 = 5, so we have the ordered pair (2, 5).
When x = -2, f(-2) = (-2)^2 + 1 = 5, so we have the ordered pair (-2, 5).
For g(x):
When x = 0, g(0) = 0^2 - 1 = -1, so we have the ordered pair (0, -1).
When x = 1, g(1) = 1^2 - 1 = 0, so we have the ordered pair (1, 0).
When x = -1, g(-1) = (-1)^2 - 1 = 0, so we have the ordered pair (-1, 0).
When x = 2, g(2) = 2^2 - 1 = 3, so we have the ordered pair (2, 3).
When x = -2, g(-2) = (-2)^2 - 1 = 3, so we have the ordered pair (-2, 3).
For f(x) + g(x):
Adding the corresponding y values from f(x) and g(x) for each x value, we get the following ordered pairs:
When x = 0, f(0) + g(0) = 1 + (-1) = 0, so we have the ordered pair (0, 0).
When x = 1, f(1) + g(1) = 2 + 0 = 2, so we have the ordered pair (1, 2).
When x = -1, f(-1) + g(-1) = 2 + 0 = 2, so we have the ordered pair (-1, 2).
When x = 2, f(2) + g(2) = 5 + 3 = 8, so we have the ordered pair (2, 8).
When x = -2, f(-2) + g(-2) = 5 + 3 = 8, so we have the ordered pair (-2, 8).