Question

For 10-11, a colony of bacteria with an initial population of 5000 grows over time t (in hours) at a rate of 16% per hour.11. How long does it take for the population to double?

Answer 1

11. The exponential function that models the growth is as follows:

`y=5000(1.16)^t`

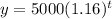
Where t is the time in hours. In this case, if we double the population we have to:

y = 5000 x 2 = 10000

Therefore, substitute y = 10000 in the function and solve for t:

`10000=5000\left(1.16\right)^t`

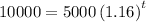
Divide both sides by 5000:

`\begin{gathered} (10000)/(5000)=(5000(1.16)^t)/(5000) \\ 2=(1.16)^t \end{gathered}`

Apply the laws of exponents:

`ln(2)=tln(1.16)`

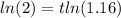
Solve for t:

`t=(ln(2))/(ln(1.16))=4.7`

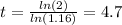
Answer: B. 4.7 hours