Question

A machine is designed to fill 16oz bottles of shampoo. When the machine is working properly, the mean amount poured into the bottles is 16.05oz with a standard deviation of 0.1oz. Assume that the machine is working properly. If four bottles are randomly selected each hour and the number of oz in each bottle is measured, then 95% of the observations should occur in which interval

Answer 1

The 95% of confidence interval are

(15.8663 ,16.2337)

Explanation:

Step(i):-

Size of the Population = 16

Size of the sample (n) = 4

The mean of the sample = 16.05 oz

The standard deviation of the sample (S) = 0.1 oz

Degrees of freedom =n-1 =4-1 =3

t₀.₀₅,₃ = 3.1824

Step(ii):-

The 95% of confidence interval is determined by

`(x^(-) - Z_(0.05) (S)/(√(n) ) , x^(-) -+Z_(0.05) (S)/(√(n) ))`

`(16.05 - 3.1824(0.1)/(√(3) ) , 16.05 -+3.1824 (0.1)/(√(3) ))`

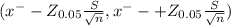
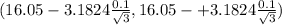
(16.05 - 0.1837 ,16.05 +0.1837 )

(15.8663 ,16.2337)

Final answer:-

The 95% of confidence interval are

(15.8663 ,16.2337)