Question

A, B & C form the vertices of a triangle.

CAB = 90°, ABC = 60° and AB = 8.6.

Calculate the length of BC rounded to 3 SF.

BC =

Answer 1

BC = 17.2.

Explanation:

Since CAB = 90º, this is a right triangle.

The triangle format is given below:

C

A B

We have that AB = 8.6, and angle B measures 60º.

Length of BC:

BC is the hypotenyse.

Side AB is adjacent to angle B = 60º.

In a right triangle, angle
`\alpha`, it's adjacent side with length s and the hypotenuse h are related by the cosine of the angle, that is:

`cos(\alpha) = (s)/(h)`

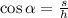
In this question, we have an angle of 60º, with has cosine 0.5. We also have that side AB = s = 8.6, and the hypotenuse h is side BC. So

`cos(\alpha) = (s)/(h)`

`0.5 = (8.6)/(h)`

`0.5h = 8.6`

`h = (8.6)/(0.5)`

`h = 17.2`

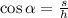
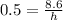
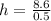
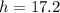
BC = 17.2.