Question

What does the constant 0.4 reveal about the rate of change of the quantity?

Answer 1

In general, the exponential growth/decay formula is

`\begin{gathered} g(x)=a(1+r)^(kx) \\ a\rightarrow\text{ intial amount} \\ r\rightarrow\text{ growth/decay} \\ k\rightarrow\text{ constant} \\ \end{gathered}`

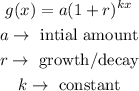
If 1+r>1, the function is growing while 1+r<1 implies that it is decaying.

In our case,

`\begin{gathered} f(t)=870(0.4)^(24t) \\ \Rightarrow(1+r)=0.4<1 \\ \Rightarrow f(t)\text{ is decaying} \end{gathered}`

Furthermore,

`\begin{gathered} 1+r=0.4 \\ \Rightarrow r=-0.6=-60\% \end{gathered}`

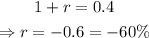
Thus, the function is decaying exponentially at a rate of 60%.

Finally, notice that t stands for the number of days; therefore, 24t implies that the function exponentially decays 60% a total of 24 times per day, and 24 times per day is equivalent to 1 time every hour.

Hence, the function decays 60% every hour.