Question

Number 17 pls and thank you Sketch and graph the equation pls

Answer 1

`y\ge-x^2-8x-12`

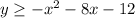
To graph the given inequality:

1. As the inequality is a quadratic inequality; find the vertex and x-intercepts of the boundary parabola:

`y=-x^2-8x-12`

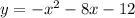
vertex:

to find the x-value of the vertex use the next formula:

`\begin{gathered} y=ax^2+bx+c \\ \\ x=-(b)/(2a) \\ \end{gathered}`
`x=-(-8)/(2(-1))=-(-8)/(-2)=-4`

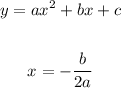
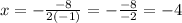
x-value in the vertex: -4

Evaluate the function of the parabola for x=-4 to find the y-value in the vertex:

`\begin{gathered} y=-(-4)^2-8(-4)-12 \\ y=-16+32-12 \\ y=4 \end{gathered}`

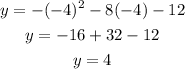
y-value in the vertex: 4

Vertex: (-4,4)

x-intercepts: Equal the function to 0 and solve x:

`\begin{gathered} -x^2-8x-12=0 \\ \\ \text{Factor:} \\ -x^2-2x-6x-12=0 \\ -x(x+2)-6(x+2)=0 \\ (x+2)(-x-6)=0 \\ \\ \\ \text{Solve x in each factor:} \\ x+2=0 \\ x=-2 \\ \\ -x-6=0 \\ -x=6 \\ x=-6 \end{gathered}`

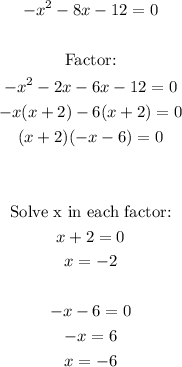
x-intercepts (-2,0) and (-6,0)

2. Use the vertex and x-intercepts to graph the parabola:

3. As the inequality sing is ≥ you shaded the area above the parabola to get the inequality graph: