Question

Kevin and Randy Muise have a jar containing 30 coins, all of which are either quarters or nickels. The total value of the coins in the jar is $4.70. How many of each typeof coin do they have?The jar contains quarters

Answer 1

Given:

The number of coins =30.

The total value of the coins in the jar is $ 4.70.

We know that quarter is worth 25 cents, nickels is worth 5 cents and a dollar is worth 100 cents.

Let x be the number of coins of the quarter.

The value of quarter =25x.

Let y be the number of coins of the nickles.

The value of nickels =5y.

`\text{ The number of coins =x+y=30}`
`x+y=30`
`x=30-y`

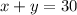
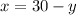
Conver the dollar into cents by multiplying 100, we get

`\text{ \$4.70=4.70}*100`

`\text{ \$4.70=47}0\text{ cents}`
`\text{The value of the coins in jar = 25x+5y=470}`
`25x+5y=470`

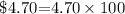
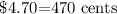
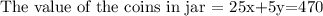
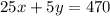
Substitute x=30-y in this equation to find the value of y.

`25(30-y)+5y=470`

`750-25y+5y=470`

`750-20y=470`

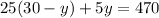
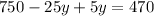
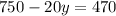
Subtracting 750 from both sides, we get

`750-20y-750=470-750`

`-20y=-280`

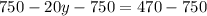
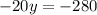
Dividing both sides by (-2), we get

`-(20y)/(-20)=-(280)/(20)`
`y=14`

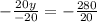
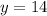
Substitute y=14 in x=30-y to find the value of x.

`x=30-14=16`

We get x=16.

Hence the number of coins of the quaters = 16 and the number of coins of the nickels =14.