Question

The tires of a car make 62 revolutions as the car reduces its speed uniformly from 90.0 km/h to 59.0 km/h. The tires have a diameter of 0.86 m.(A) What was the angular acceleration of the tires? (B) If the car continues to decelerate at this rate, how much more time is required for it to stop? (C) If the car continues to decelerate at how far does it go? Find the total distance.

Answer 1

Answer:

A) Angular acceleration = -2.47 rad/s²

B) 23.54 seconds

C) The total distance covered = 294.23m

Explanations:

The number of revolutions = 62

Angular distance, θ = 62 x 2π

θ = 62 x 2 x 3.142

θ = 389.608 radians

Diameter, d = 0.86 m

Radius, r = d/2 = 0.86/2

r = 0.43m

Initial velocity, v₁ = 90 km/h = 90 x (1000/3600)

v₁ = 25 m/s

Angular velocity, w₁ = v₁ / r

w₁ = 25/0.43

w₁ = 58.14 rad/s

Final velocity, v₂ = 59 km/h = 59 x (1000/3600)

v₂ = 16.39 m/s

Angular velocity, w₂ = v₂ / r

w₂ = 16.39 / 0.43

w₂ = 38.12 rad/s

Using the equation of motion:

`\begin{gathered} w^2_2=w^2_1\text{ + 2}\alpha\theta \\ 38.12^2=58.14^2\text{ + 2}\alpha(389.608) \\ 38.12^2-58.14^2=\text{ }779.216\alpha \\ 779.216\alpha\text{ = }-1927.1252 \\ \alpha\text{ = }(-1927.1252)/(779.216) \\ \alpha\text{ = }-2.47rad/s^2 \end{gathered}`

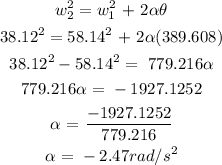
Angular acceleration = -2.47 rad/s²

B) Amount of time required for the car to stop if it continues to decelerate at this rate

Initial angular speed, w₁ = 58.14 rad/s

When the car stops, final angular speed, w₂ = 0 rad/s

Using the equation of motion below:

`\begin{gathered} w_2=w_1+\text{ }\alpha t \\ 0\text{ = 58.14 + (-2.47)t} \\ -2.47t\text{ = -58.14} \\ t\text{ = }(-58.14)/(-2.47) \\ t\text{ = }23.54\text{ seconds} \end{gathered}`

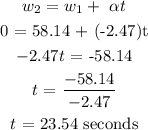
C) The total distance

Use the equation of motion below:

`\begin{gathered} S=v_1\text{t + }(1)/(2)at^2 \\ a\text{ = }\alpha r \\ a\text{ = (-2.47)(0.43)} \\ a\text{ = }-1.0621m/s^2 \end{gathered}`
`\begin{gathered} S=v_1\text{t + }(1)/(2)at^2 \\ S\text{ = }25(23.54)+0.5(-1.0621)(23.54)^2 \\ S\text{ = }588.5-294.27 \\ S\text{ = }294.23\text{ m} \end{gathered}`

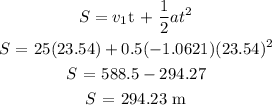
The total distance covered = 294.23m