Question

Which of the following describes how to translate the graph y = |x| to obtain the graph of y = |x| - 4?

4 units up

4 units down

4 units left

4 units right

Answer 1

the answer is that it goes 4 units down, i hope this helped :D

Answer 2

4 units down

Explanation:

Translations are transformations that change the position of the graph of a function. The general form of the graph of a function is moved up, down, right or left

Given a function:

`y=f(x)`

A vertical translation can be expressed as:

`y=f(x)+c=Vertical\hspace{3}translation\hspace{3}c\hspace{3}units\hspace{3}up\\y=f(x)-c=Vertical\hspace{3}translation\hspace{3}c\hspace{3}units\hspace{3}down`

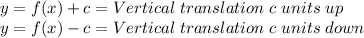
Where:

`c=constant>0`

So:

`y=|x|-4`

It's a vertical translation 4 units down. You can corroborate checking the picture I attached you and evaluating the function at x=0

`y(0)=|0|-4=-4`