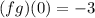Given:
The functions given are,
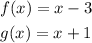
Required:
To find the value of
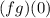
Step-by-step explanation:
We have two given functions as:
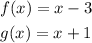
Therefore, the product of two functions is given by,
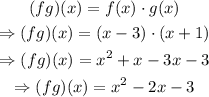
Thus, the value of the product of the functions at x = 0 is,
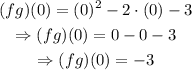
Final Answer:
The value of the product of the functions at x = 0 is,