Let the width be x and the length be y as shown in the figure.
The perimeter of the fence is 246 feet so it follows:
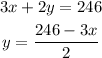
The area of the fence is given by:
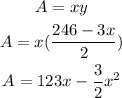
Differentiate w. r. t. x to get:

For maxima and minima calculation, the derivative is zero so it follows:
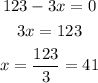
So the width is 41 feet and the length y is given by:
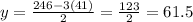
So the width is 41 feet and length is 61.5 feet, the area covered is 2521`.5 sq feet.