Answer:
the common difference = 4
Explanation:
First term of an arithmatic sequence is -3
15th term is 53
We need to find the common difference 'd'
Formula for nth term of the sequence is
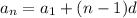
where a_1 is the first term and d is the common difference
a1= -3
Lets plug in 15 for n
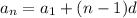
 , solve for d
, solve for d
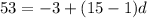
Add 3 on both sides
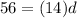
Divide both sides by 14
d=4
So, the common difference = 4