SOLUTION
We want to get a degree 3 polynomial with zeros at

This polynomial can be interpreted as
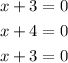
Writing as a function we have
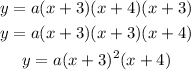
So, now we need to find the value of a from the point (0, 12), so here x = 0 and y = 12, we have
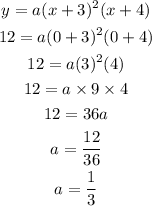
Placing the value of a into the equation

We have
![undefined]()