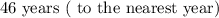SOLUTION:
Step 1:
In this question, we are given the following:
A country's population is described by the model:
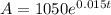
where t is years.
How long will it take the population to double?
Round off to the nearest year.
Step 2:
Now, double the population means that:
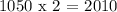
Then, we have that:
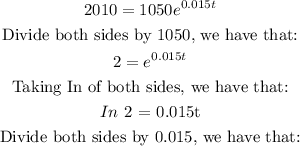
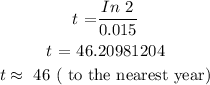
CONCLUSION:
The final answer is: