Answer:
Quadrilateral ABCD is not a rectangle, square, or parallelogram because both pairs of opposite sides are not parallel or congruent.
Explanation:
Consider quadrilateral ABCD with its vertices at:
A(2, 1), B(2, 4), C(7, 4), and D(6, 1).
Line AD is a horizontal line passing through y=1.
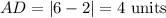
Similarly, line BC is a horizontal line passing through y=4.
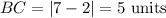
Since the opposite sides are not equal, the quadrilateral ABCD is not a rectangle, square, or parallelogram because both pairs of opposite sides are not parallel or congruent.
The last option is correct.
Note: The result can be confirmed from the graph below: