Question

Mrs. Decker saw three witches land in a field where they found a pile of pumpkins and a ghost. They agree to sleep overnight in the field and divide up the pile of pumpkins in the morning. During the night, one witch wakes up, gives one pumpkin to the ghost, takes exactly 1/3 of the rest of the pumpkins and falls back asleep. Then second witch wakes up and does the same thing. Later, the third witch wakes up and does the same. In the morning there are fewer than 10 pumpkins left. They each take 1/3. How many pumpkins were there in the original pile?

Answer 1

`x`-total number of pumpkins

First witch took
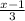
`(x-1)/(3)` pumpkins.

The number of pumpkins remained
`2(x-1)/(3) = (2(x-1))/(3) = (2x-2)/(3)`

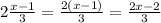
Second witch took
`((2x-2)/(3)-1)/(3) = (2x-5)/(9)`

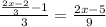
The number of pumpkins remained
`2(2x-5)/(9)= (4x-10)/(9)`

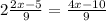
Third witch took
`((4x-10)/(9)-1)/(3) = (4x-19)/(27)`

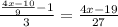
Ghost took 3 pumpkins. The number of pumpkins remained is 3,6 or 9.

Solve equation for each case.

1)
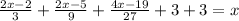
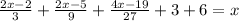
`(2x-2)/(3)+(2x-5)/(9)+(4x-19)/(27)+3+3=x`

2)
`(2x-2)/(3)+(2x-5)/(9)+(4x-19)/(27)+3+6=x`

3)
`(2x-2)/(3)+(2x-5)/(9)+(4x-19)/(27)+3+9=x`

Only equation 2) has a solution which is a whole number: 25

The total number of pumpkins is 25.