Observe the given probability density function (PDF) carefully.
The function is constant and spans from x=0 to x=2.
The probability of the random variable lying in an interval is given by the area under the PDF corresponding to that interval.
Since the total probability is always unity in the entire domain of the PDF. The total area of the rectangle must be unity.
Let 'c' be the height of the rectangle, then equating the total area to unity,
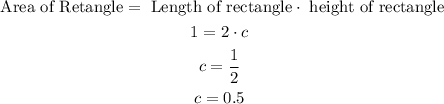
Now that we know the height of the rectangle is 0.5, so the probability that the value of random variable X is at least 1.28 is equal to the area under the curve beyond x = 1.28,
[tex]\begin{gathered} P(X\ge1.28)=\text{Area}(X\ge1.28) \\ P(X\ge1.28)=\text{Area}(1.28\leq X\leq2)+\text{Area}(2Thus, the required probability is
0.36 or
36%.