Question

For the polynomial –2m2n3 + 2m?n3 + 7n2 – 6m4 to be a binomial with a degree of 4 after it has been fully simplified, which must be the missing exponent on the m-term? 0 1 2 4

Answer 1

C. 2

Step-by-step explanation:

I just got it right on Edge.

Hope it helps!

Answer 2

Option (c) is correct.

power of m has to be 2.

Step-by-step explanation:

Given : Polynomial
`-2m^2n^3+2m^((x))n^3+7n^2-6m^4`

We have to find the value of x so that the given polynomial has to be a binomial with a degree of 4 after it has been fully simplified.

Consider the given polynomial
`-2m^2n^3+2m^((x))n^3+7n^2-6m^4`

We call a polynomial a binomial if it has two terms.

And for degree 4 the greatest power of variables in an term must have to be 4.

Thus, for given polynomial to be a binomial with a degree of 4.

The degree of
`-2m^2n^3` and
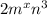`2m^(x)n^3` has to be same so that they get cancel out and we are left with two terms and
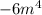`-6m^4` will have the highest degree 4.

Thus, power of m has to be 2.

Thus, when power of m is 2 , then

`-2m^2n^3+2m^(2)n^3+7n^2-6m^4`

`\Rightarrow -2m^2n^3+2m^(2)n^3+7n^2-6m^4`

`\Rightarrow 7n^2-6m^4`

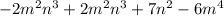
Which is a binomial with a degree of 4 after it has been fully simplified.