Given the points (1, 12) and (-1, 0.75)
We will write the exponential function that includes the given points
Let the expression of the function will be as follows:
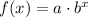
When x = 1, f = 12
so,

When x = -1, f = 0.75
So,
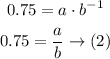
Solve the equations (1) and (2) to find (a) and (b)
Multiply the equations to eliminate (b)
![\begin{gathered} 12\cdot0.75=a^2 \\ a^2=9 \\ a=\sqrt[]{9}=3 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/hpu584m8qj6pyzn1r7x2.png)
Substitute with (a) into equation (1) to find (b)
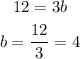
So, the answer will be:
The equation of the exponential function will be as follows:
