Answer:
h '= [ ( \frac{ M-m}{M +m } )+ 2 (\frac{M}{M+m})]² h
Step-by-step explanation:
Let's analyze this problem, first the two bodies travel together, second the superball bounces, third it collides with the marble and fourth the marble rises to a height h ’
let's start by finding the velocity of the two bodies just before the collision, let's use the concepts of energy
starting point. Starting point
Em₀ = U = m g h
final point. Just before the crash
Em_f = K = ½ m v²
as there is no friction the mechanical energy is conserved
Em₀ = Em_f
mg h = ½ m v²
v = √2gh
this speed is the same for the two bodies.
Second point. The superball collides with the ground, this process is very fast, so we will assume that the marble has not collided, let's use the concept of conservation of moment
initial instant. Just when the superball starts contacting the ground
p₀ = M v
this velocity is negative because it points down
final instant. Just as the superball comes up from the floor
p_f = M v '
the other body does not move
p₀ = p_f
- m v = M v '
v ’= -v
Therefore, the speed of the asuperbola is the same speed with which it arrived, but in the opposite direction, that is, upwards.
Let's use the subscript 1 for the marble and the subscript 2 for the superball
Third part. The superball and the marble collide
the system is formed by the two bodies, so that the forces during the collision are internal and the moment is conserved
initial instant. Moment of shock
p₀ = M
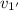 + m v_2
+ m v_2
final instant. When the marble shoots out.
P_f = Mv_{1f'}+ m v_{2f}
p₀ = p_
M v_{1'}+ m v_2 = M v_{1f'} + m v_{2f}
M (v_{1'} - v_{1f'}) = -m (v_2 - v_{2f})
in this expression we look for the exit velocity of the marble (v2f), as they indicate that the collision is elastic the kinetic nerve is also conserved
K₀ = K_f
½ M v_{1'}² + m v₂² = M v_{1f'}² + ½ m v_{2f}²
M (v_{1'}² - v_{1f'}²) = - m (v₂² - v_{2f}²)
Let's set the relation (a + b) (a-b) = a² - b²
M (v_{1'} + v_{1f'}) (v_{1'} - v_{1f'}) = -m (v₂ + v_{2f}) (v₂ - v_{2f})
let's write our two equations
M ( v_{1'} - v_{1f'}) = -m (v₂ - v_{2f}) (1)
M (v_{1'} + v_{1f'}) (v_{1'} - v_{1f'}) = -m (v₂ + v_{2f}) (v₂ - v_{2f})
if we divide these two expressions
(v_{1'}+ v_{1f'}) = (v₂ + v_{2f} )
we substitute this result in equation 1 and solve
v_{1f'}= (v₂ + v_{2f}) - v_{1'}
M (v_{1'} - [(v₂ + v_{2f}) - v_{1'}] = -m (v₂ - v_{2f})
-M v₂ - M v_{2f1'} + 2M v_{1'} = m v₂ - m v_{2f}
-M v_{2f} -m v_{2f} = m v₂ -M v₂ + 2M v_{1'}
v_{2f} (M + m) = - v₂ (M-m) + 2 M v_{1'}
v_{2f} = -
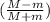 ) v₂ + 2
) v₂ + 2
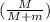 v_{1'}
v_{1'}
now we can substitute the velocity values found in the first two parts
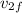 = - ( \frac{ M-m}{M +m } ) √2gh + 2(\frac{M}{M+m}) √2gh
= - ( \frac{ M-m}{M +m } ) √2gh + 2(\frac{M}{M+m}) √2gh
we simplify
v_{2f} = [( \frac{ M-m}{M +m } ) + 2 (\frac{M}{M+m})]
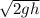
let's call the quantity in brackets that only depends on the masses
A = ( \frac{ M-m}{M +m } )+ 2 (\frac{M}{M+m})]
v_{2f}= A \sqrt{2gh}
in general, the marble is much lighter than the superball, so its speed is much higher than the speed of the superball
finally with the conservation of energy we find the height that the marble reaches
Starting point
Emo = K = ½ mv_{2f}²
Final point
Emf = U = m g h'
Em₀ = Em_f
½ m v_{2f}² = m g h ’
h ’= ½ v_{2f}² / g
h ’= ½ (A \sqrt{2gh})² / g
h ’= A² h
h '= [ ( \frac{ M-m}{M +m } )+ 2 (\frac{M}{M+m})]² h