Question

The figure shows a small plane flying at a speed of 178 miles per hour on a bearing of N40°E. The wind is blowing from west to east at 47 miles per hour. The figure indicates that v represents the velocity of the plane in still air and w represents the velocity of the wind.(c)What would be the ground speed? (nearest tenth round)

Answer 1

`A\text{. }v=178\cos 50\degree i+178\sin 50\degree j,w=47\cos 0\degree i+47\sin 0\degree j`

Part B: v+w=161.42i+136.36j

Part C: 211.3 mph

Explanation:

Part A

• The velocity of the plane in still air, v = 178 miles per hour.

,

• The angle v makes with the x-axis = 90°-40° = 50°

Therefore, vector v in terms of its magnitude and direction cosine is:

`v=178\cos 50\degree i+178\sin 50\degree j`

Similarly:

• The velocity of the wind, w = 47 miles per hour.

,

• The angle w makes with the x-axis = 0°

Therefore, vector w in terms of its magnitude and direction cosine is:

`w=47\cos 0\degree i+47\sin 0\degree j`

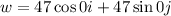
The correct option is A.

Part B

From part A:

`\begin{gathered} v=178\cos 50\degree i+178\sin 50\degree j=\langle114.42,136.36\rangle \\ w=47\cos 0\degree i+47\sin 0\degree j=\langle47,0\rangle \end{gathered}`

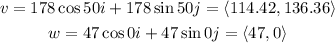
Therefore, the resultant vector, v+w is:

`\begin{gathered} v+w=\langle114.42,136.36\rangle+\langle47,0\rangle \\ Add\text{ the respective components} \\ =\langle114.42+47,136.36+0\rangle \\ =\langle161.42,136.36\rangle \\ v+w=161.42i+136.36j \end{gathered}`

Part C

The magnitude of v+w, called the ground speed, gives its speed relative to the ground.

`\mleft\Vert v+w\mright||=√(161.42^2+136.36^2)=211.3\; \text{mph}`

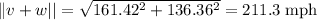
The ground speed is 211.3 mph (rounded to the nearest tenth).