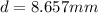Answer:
Step-by-step explanation:
From the question we are told that
Pressurized air pressure is
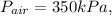
Atmospheric pressure is
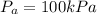
Initial acceleration of the water rocket is
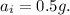
Acceleration of the water rocket is
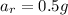
Mass of water is
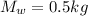
Generally total mass is given mathematically given as
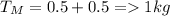
Generally the tension on the rocket is given mathematically given as
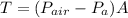
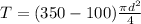
T is also
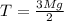
Therefore

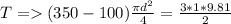
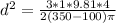
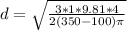
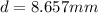
therefore diameter of nozzle is mathematically given as