Question

The graph of a quadratic function increases through interval A, then decreases through interval B. If the vertex of thegraph is located at (5,9), which equation could represent this function?Interval A: -00<<5Interval B:5 <

Answer 1

Since the function increases when x goes from -∞ to 5, and decreases when x goes from 5 to ∞, then the parabola has a maximum at its vertex, therefore it is a concave down parabola.

The general form of a concave down parabola, with vertex (5,9) is:

`\begin{gathered} y-9=-k(x-5)^2, \\ \text{where k is a positive constant.} \end{gathered}`

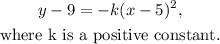
Answer: Option d)

`f(x)=-(x-5)^2+9.`