Question

Which statement is NOT true?

If x = 1, then x2 = 1.
If x = –1, then x2 = 1.
x2 = 1 if and only if x = 1 or x = –1.
If x2 = 1, then x = 1.

Answer 1

is the "2" an exponent

Answer 2

Answer: The statement that is not true is

(D) If x² = 1, then x = 1.

Step-by-step explanation: We are given to select the statement that is NOT true.

Statement 1 : If x = 1, then x² = 1.

Let x = 1, then we have

`x^2=1^2=1.`

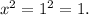
So, the statement is TRUE.

Statement 2 : If x = -1, then x² = 1.

Let x = -1, then we have

`x^2=(-1)^2=1.`

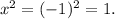
So, the statement is TRUE.

Statement 3 : x² = 1 if and only if x = 1 or x = –1.

Let x = 1 or -1, then we have

`x^2=1^2=1,\\\\x^2=(-1)^2=1.`

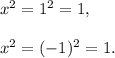
Again, let x² = 1, then

`x^2=1\\\\\Rightarrow x=\pm√(1)~~~~~~~~~[\textup{taking square root on both sides}]\\\\\Rightarrow x=1,~-1.`

So, x² = 1 if and only if x = 1 or x = –1.

That is, the statement is TRUE.

Statement 4 : If x² = 1, then x= 1.

Let x² = -1, then we have

`x^2=1\\\\\Rightarrow x=\pm√(1)~~~~~~~~~[\textup{taking square root on both sides}]\\\\\Rightarrow x=1,~-1.`

So, if x² = 1, then x = 1 or x = –1.

Therefore, the statement is NOT TRUE.

Thus, the statement that is not true is (D).