Question

Consider the following reaction… 5C + 2SO2 CS2 + 4CO a) How many moles of CS2 would be produced by reacting 9.50 moles of SO2 with an excess of C? _________________ b) How many grams of C would be needed to fully react 5.5 L of SO2 at STP? _________________ c) How many liters of CO can be produced from 20.0 moles of C at STP?

Answer 1

The calculation involves using the stoichiometry of the given balanced chemical equation to determine moles of CS₂ produced, grams of carbon needed, and liters of CO produced at STP. The answers are 4.75 moles, 7.37 grams, and 358.4 liters respectively.

Step-by-step explanation:

To solve the given stoichiometry problems related to the chemical reaction of carbon (C) with sulfur dioxide (SO₂), we first need to refer to the balanced chemical equation provided and use stoichiometry principles to determine the moles and grams of various substances produced or needed in a reaction.

a) According to the balanced chemical equation, 2 moles of SO₂ produce 1 mole of CS₂. Therefore, for 9.50 moles of SO₂, the moles of CS₂ produced would be:

• 9.50 moles SO₂ × (1 mole CS₂ / 2 moles SO₂)
• = 4.75 moles of CS₂

b) Using the ideal gas law (PV = nRT), and knowing that at STP 1 mole of gas occupies 22.4 L, we can determine the moles of SO₂: 5.5 L SO₂ × (1 mole SO₂ / 22.4 L) = 0.2455 moles of SO₂. Now, using the stoichiometry of the balanced equation, where 2 moles of SO₂ require 5 moles of C, we find the moles of C needed:

• 0.2455 moles SO₂ × (5 moles C / 2 moles SO₂) = 0.6138 moles of C.
• To get grams of C:
• 0.6138 moles C × (12.01 g/mol) = 7.37 grams of C.

c) From the balanced chemical equation, 5 moles of C produce 4 moles of CO. Therefore, for 20.0 moles of C, the liters of CO produced at STP would be:

• 20.0 moles C × (4 moles CO / 5 moles C) = 16.0 moles of CO.
• Converting to liters at STP:
• 16.0 moles CO × (22.4 L / mole) = 358.4 liters of CO.

Answer 2

We first verify that the equation is balanced. We have 5 carbons (C), 2 sulfurs (S), and 4 oxygens (O) on each side of the reaction. So the reaction is balanced.

a) Now if we look at the reaction we can see that when 2 moles of SO2 react, 1 mole of CS2 is produced. That is, the ratio is 2 to 1. For each mole of SO2 half as many moles of CS2 will be produced.

So if we have 9.5 moles of SO2 we will have 9.5/2 moles, that is 4.75 moles of CS2.

Answer a) By reacting 9.50 moles of SO2 with an excess of it would be produced 4.75 moles of CS2.

Now, for the following parts of the question, we can apply the ideal gas law. This is because the reaction is in the gas phase and the law applies only to gases.

`PV=nR_{}T`

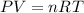
Where,

P= Pressure at STP = 1 atm

T= Temperature at STP = 273.15K

R= Ideal law constant = 0.08206 (atm L)/(mol K)

V= Volume of the gas

n= Numer of moles

b)We clear n and we replace the known values of SO2 to find the number of moles of SO2 that react.

`\begin{gathered} n=(PV)/(RT)=\frac{1at_{}m*5.5L}{0.08206\frac{atm.L}{\text{mol}\mathrm{}K}*273.15K} \\ n=0.24mol\text{ SO}_2 \end{gathered}`

Now, for each mole of SO2 that reacts we need 5/2 moles of C, that is 0.24x5/2=0.61 moles of C.

We use mass molar of C to calculate the grams.

Mass molar of C=12.01g/mol

Mass of C= Moles of C x Mass Molar

Mass of C= 0.61 mol x 12.01 g/mol = 7.37 g

So, To fully react 5.5 L of SO2 at STP we will need 7.37 g of C.

c)We apply the gas law again but this time we clear the volume.

We also take into account that for each mole of C, 4 moles of CO are produced, so if we have 20 moles of C we will produce 20x4=80 moles of CO.

`\begin{gathered} V=(nRT)/(P) \\ V=(80mol*0.08206(atm.L)/(mol.K)*273.15K)/(1atm) \\ V=\text{ 1793.18 L} \end{gathered}`

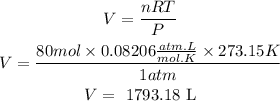
So, from 20.0 moles of C at STP can be produced 1793.18 liters of CO