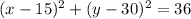Question

The subject is pre calculus I have a question from my prep guide that I need answered I provided a picture

Answer 1

You know that the length and the width of the rectangular backyards are:

`\begin{gathered} l=600ft \\ w=300ft \end{gathered}`

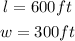
Knowing the coordinates of the vertices of the rectangle, you can plot them on a Coordinate Plane and draw the rectangle. Notice that the vertices are:

`\mleft(0,0\mright),\mleft(0,60\mright),\mleft(30,60\mright),\mleft(30,0\mright)`

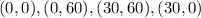
See the picture below:

According to the information given in the exercise, a circular flower garden is dug to be exactly in the center of the backyard. The radius of this circle is:

`r=60ft`

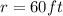
If you draw the diagonals of the rectangle, you can find its center and therefore, the center of the circle. See the picture below:

Now you know the center of the circle.

By definition, the equation of a circle is:

`\mleft(x-h\mright)^2+\mleft(y-k\mright)^2=r^2`

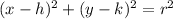
Where "r" is the radius of the circle and its center is:

`(h,k)`

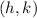
Since you already know the center of the circular flower garden and its radius, you only need to substitute values into the equation and simplify:

`\begin{gathered} (x-15)^2+(y-30)^2=6^2 \\ (x-15)^2+(y-30)^2=36 \end{gathered}`

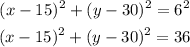
Therefore, the answer is:

`(x-15)^2+(y-30)^2=36`