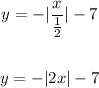When we horizontally shrink a function by a factor k, we multiply the variable x, in the expression of the function, by k:
y = f(x) -> y' = f(kx)
When the factor k is greater than 1, that will represent in fact a horizontal shrink of the graph. But, since the factor we need to apply is less than 1, the result of horizontally shrinking the graph will effectively be a horizontal stretch.
First, let's reflect the function y = |x| over the x-axis. This changes the sing of y:
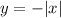
Now, we need to multiply the variable x by 1/2 to horizontally shrink the graph by 1/2:
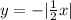
Now, we need to translate the graph 7 units down. So, we need to subtract 7 from the final expression for y:
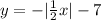
Notice the result of those transformations:
Notice that, strictly, a horizontal shrink of 1/2 is actually a horizontally stretch of 2.
Now, if what the exercise really means is that the graph is in fact horizontally shrunk, then you need to divide the variable x by 1/2. This results in the function