Question

In a box there a total of four prizes: Two of them are worth $4, a single prize worth $21, and a single prize worth $164. A player will reach into the box and draw one of the prizes at random. What is the fair price for this game?

Answer 1

Let's start by calculating the expected value for this game.

Let's call X to the random variable : ''The earnings for this game''

We calculate E(X) by multiplying the probability of the random variable assuming the value ''xi'' by the prize for ''xi'' and adding for all its values.

There is a total of 4 prizes.

2 prizes out of a total of 4 worth $4.

1 prizes out of a total of 4 worth $21

1 prize out of a total of 4 worth $164.

`E(X)=(2)/(4)*4+(1)/(4)*21+(1)/(4)*164`
`E(X)=(8+21+164)/(4)=(193)/(4)=48.25`

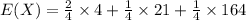
The expected value for X is $48.25

Therefore, its reasonable set the ''fair price'' in $48.25 for this game.