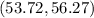Question

In a sample of 200 households, the mean number of hours spent on social networking sites during the month of January was 55 hours. In a much larger study, the standard deviation was determined to be 7 hours. Assume the population standard deviation is the same. What is the 99% confidence interval for the mean hours devoted to social networking in January?

Answer 1

Answer: 99% confidence interval is given by
`(53.72,56.27)`

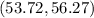
Explanation:

Since we have given that

Number of households in a sample = 200

Mean number of hours spent on social networking sites during the month of January = 55 hours

Standard deviation = 7 hours

Since we have given that the population standard deviation is the same.

and there is 99% confidence interval for the mean hours devoted to social networking in January.

According to the critical value table we get that

α = tail area = 0.05

central area = 1-2α = 0.99 (99% confidence interval)

So, critical value will be
`z_(0.05)=2.58`

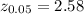
As we know that

Margin error = Standard error × critical value

where , Standard error =
`(\sigma)/(√(n))=(7)/(√(200))=0.495`

so, Margin error becomes

`0.495* 2.58\\\\\approx \pm 1.28`

So, 99% confidence interval is given by

`(53.72,56.27)`

Answer 2

99% Confidence Interval = 55 + or - 2.58 x 7/sqrt(200) = 55 + or - 2.58 x 0.495 = 55 + or - 1.277 = 53.773 or 56.227