Answer: 0.25
Explanation:
Given : A fair coin is tossed twice in succession.
The set of equally likely outcomes is {HH, HT, TH, TT}.
i.e. The total number of outcomes = 4
In order to get exactly two tails , the total number of favorable outcomes = 1 (TT)
We know that ,
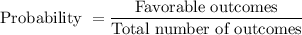
Then, the probability of getting exactly two tails =
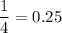
Hence, the required probability = 0.25