Question

Which of the following shows the extraneous solution to the logarithmic equation below? log3(18x^3)-log3(2x)=log3(144). A. x=-16 B. x=-8 C. x=-4 D. x=-2

Answer 1

Option C. x = -4

Explanation:

We have to find the extraneous solution of the given logarithmic equation.

`log_(3)(18x^(3))-log_(3)(2x)=log_(3)(144)}`

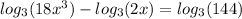
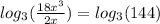`log_(3)((18x^(3))/(2x))=log_(3)(144)` [Since log (
`(a)/(b)`)=log a - log b ]

Now
`(18x^(3) )/(2x)=144`

`9x^(2) =144`⇒
`x^(2) =(144)/(9)=16`

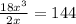
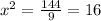
x = ±4

Now we put x = 4 in the logarithmic equation

`log_(3)(18* 4^(3))-log_(3)(2* 4)=log_(3)(144)`

`log_(3)((18* 64)/(8))=log_(3)(144)`

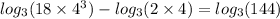
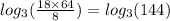
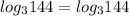`log_(3) 144=log_(3)144` So x = 4 is the real solution

Now we put x = -4 in the logarithmic equation

`log_(3)[18(-4)^(3)]-log_(3)[2(-4)]=log_(3)(144)`

`log_(3)(-1152)-log_(3)(-8)=log_(3)(144)`

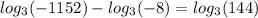
Since logarithm of any negative number is not defined so x = -4 will be the extraneous solution.

Answer 2

log3(18x^3) - log3(2x) = log3(144)
log3(18x^3/2x) = log3(144)
9x^2 = 144
x^2 = 144/9 = 16
x = 4 or x = - 4

x = -4 is the extraneous solution.