Answer:
17.22 g s the amount of
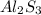 remains.
remains.
Step-by-step explanation:
Moles of
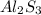 :-
:-
Mass = 20.00 g
Molar mass of
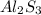 = 150.17 g/mol
= 150.17 g/mol
The formula for the calculation of moles is shown below:

Thus,
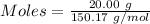
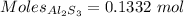
Moles of
 :-
:-
Mass = 2.00 g
Molar mass of
 = 18.02 g/mol
= 18.02 g/mol
The formula for the calculation of moles is shown below:

Thus,
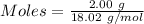
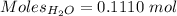
According the given reaction:-
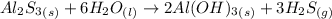
1 mole of
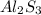 reacts with 6 moles of
reacts with 6 moles of

0.1332 mole of
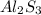 reacts with 0.1332*6 moles of
reacts with 0.1332*6 moles of

Moles of
 required = 0.7992 mol
required = 0.7992 mol
Available moles of
 = 0.1110 mol
= 0.1110 mol
Limiting reagent is the one which is present in small amount. Thus,
 is limiting reagent.
is limiting reagent.
The formation of the product is governed by the limiting reagent. So,
6 moles of
 reacts with 1 mole of
reacts with 1 mole of
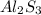
Also,
1 mole of
 reacts with 1/6 mole of
reacts with 1/6 mole of
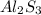
0.1110 mole of
 reacts with
reacts with
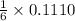 mole of
mole of
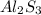
Moles of
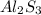 reacted = 0.0185 moles
reacted = 0.0185 moles
Thus, moles of
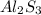 unreacted = 0.1332 moles - 0.0185 moles = 0.1147 moles
unreacted = 0.1332 moles - 0.0185 moles = 0.1147 moles
Moles of
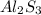 unreacted = 0.1147 moles
unreacted = 0.1147 moles
Mass = Moles*Molar mass = 0.1147moles*150.17 g/mol = 17.22 g
17.22 g s the amount of
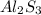 remains.
remains.