The price we would be willling to pay is equivalent to the present value (P) calculated using the discount rate for each case.
The future value (A) is equal to $2000 and the period is t = 10 years.
We can relate the present value with the future value with the formula:
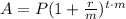
a) For this case we have:
r = 0.05
m = 12 (monthly compound)
t = 10 years
A = 2000
Then, we can calculate P as:
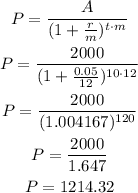
The price we would be willing to pay today at this discount rate is $1214.32.
b) In this case, r is r = 0.04 and it is compounded continously. In this case, we have to use another equation for continously compounded interest:
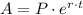
For this case, we have:
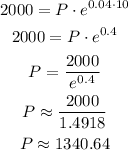
The price we would be willing to pay today at this discount rate is $1340.64.
Answer:
a) $1214.32
b) $1340.64